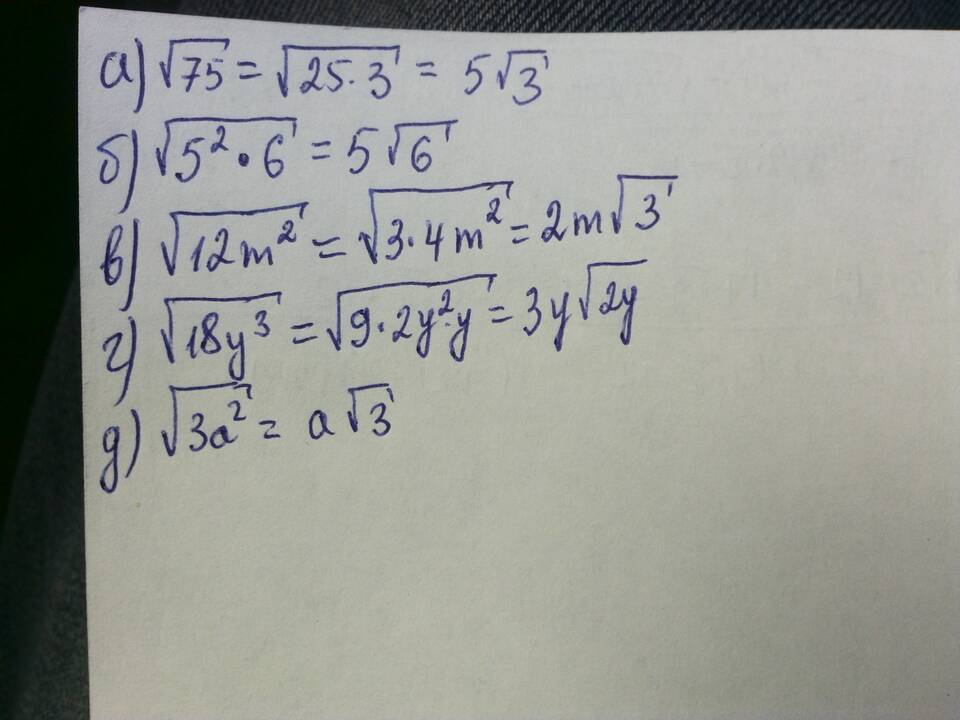Выражения под корнем часто встречаются в математике, и умение их правильно выводить важно для упрощения уравнений и решения задач. В этой статье рассмотрим основные методы вынесения множителей из-под корня.
Содержание
Основные понятия
Корень n-ной степени из числа a обозначается как √na. Чаще всего используются квадратные корни (n=2) и кубические корни (n=3). Чтобы вынести множитель из-под корня, необходимо разложить подкоренное выражение на множители.
Вынесение множителя из-под квадратного корня
Для квадратного корня √a·b действует правило:
- √(a·b) = √a · √b
Пример:
- √50 = √(25·2) = √25 · √2 = 5√2
Алгоритм вынесения множителя:
- Разложите подкоренное число на множители, один из которых — полный квадрат.
- Извлеките корень из полного квадрата.
- Запишите результат в виде произведения корней.
Вынесение множителя из-под корня n-ной степени
Для корня n-ной степени √n(a·b) правило аналогично:
- √n(a·b) = √na · √nb
Пример:
- ∛54 = ∛(27·2) = ∛27 · ∛2 = 3∛2
Алгоритм:
- Разложите подкоренное выражение на множители, один из которых — полная степень n.
- Извлеките корень n-ной степени из этого множителя.
- Запишите результат.
Примеры для разных случаев
| Исходное выражение | Разложение | Результат |
| √72 | √(36·2) | 6√2 |
| ∛16 | ∛(8·2) | 2∛2 |
| √(x3) | √(x2·x) | x√x |
Заключение
Вынесение множителя из-под корня — важный навык, который помогает упрощать выражения и решать уравнения. Главное — правильно разложить подкоренное выражение на множители и применить свойства корней.