В геометрии существует фундаментальное свойство треугольников, касающееся суммы их внутренних углов. Это свойство является одним из базовых принципов евклидовой геометрии.
Содержание
Основная теорема о сумме углов треугольника
Сумма внутренних углов любого треугольника всегда равна 180 градусам. Это правило верно для всех типов треугольников в евклидовой геометрии.
| Тип треугольника | Сумма углов |
| Остроугольный | 180° |
| Прямоугольный | 180° |
| Тупоугольный | 180° |
| Равносторонний | 180° |
| Равнобедренный | 180° |
Доказательство теоремы
Существует несколько способов доказательства этой теоремы:
- Через параллельные прямые и свойства накрест лежащих углов
- С помощью измерения углов транспортиром
- Путем разрезания треугольника и составления углов в прямую линию
Классическое доказательство
- Проводим прямую, параллельную одной из сторон треугольника
- Используем свойства соответственных и накрест лежащих углов
- Образовавшиеся углы в сумме дают развернутый угол (180°)
Практическое применение
Знание суммы углов треугольника позволяет:
| Нахождение неизвестного угла | Если известны два угла, третий вычисляется как 180° минус сумма известных |
| Проверка построения | Контроль правильности построения треугольников |
| Решение геометрических задач | Основа для доказательства других теорем |
Пример расчета
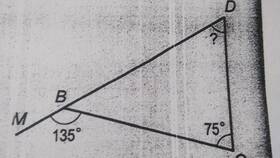
В треугольнике ABC известны углы: ∠A = 45°, ∠B = 60°. Найдем ∠C:
- Сумма известных углов: 45° + 60° = 105°
- Неизвестный угол: 180° - 105° = 75°
Исключения в неевклидовой геометрии
В геометрии Лобачевского (гиперболической геометрии) сумма углов треугольника:
- Всегда меньше 180°
- Зависит от площади треугольника
- Разница между 180° и суммой углов называется дефектом
В сферической геометрии сумма углов треугольника всегда больше 180° и также зависит от площади фигуры.