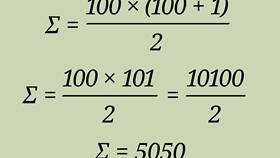Вычисление суммы - базовая математическая операция, имеющая определенные правила и свойства. Рассмотрим основные принципы сложения чисел и других математических объектов.
Содержание
Основные правила сложения
| Правило | Формулировка | Пример |
| Коммутативность | От перемены мест слагаемых сумма не меняется | a + b = b + a |
| Ассоциативность | Группировка слагаемых не влияет на результат | (a + b) + c = a + (b + c) |
| Нейтральный элемент | Прибавление нуля не изменяет число | a + 0 = a |
Правила сложения различных типов чисел
Целые числа
- Сложение чисел с одинаковыми знаками: складываем модули, сохраняем знак
- Сложение чисел с разными знаками: вычитаем из большего модуля меньший, ставим знак большего
Дроби
- Привести дроби к общему знаменателю
- Сложить числители
- Знаменатель оставить без изменения
Десятичные дроби
| Действие | Пример |
| Записать числа друг под другом, выравнивая по запятой | 12,34 + 5,6 = 12,34 + 5,60 |
| Сложить поразрядно | 12,34 + 5,60 = 17,94 |
Правила суммирования в математическом анализе
- Сумма бесконечного ряда может быть конечной (сходящийся ряд)
- Абсолютно сходящиеся ряды можно переставлять
- Условно сходящиеся ряды требуют осторожности при перестановке
Свойства суммирования
| Свойство | Формула |
| Дистрибутивность умножения относительно сложения | a × (b + c) = a×b + a×c |
| Правило вынесения общего множителя | a×b + a×c = a × (b + c) |
| Правило почленного сложения неравенств | Если a > b и c > d, то a + c > b + d |
Правила суммирования в программировании
- Учет переполнения при работе с целыми числами
- Погрешности округления при сложении чисел с плавающей точкой
- Оптимизация последовательного суммирования
- Использование специальных алгоритмов для больших массивов
Практические рекомендации
- При сложении больших чисел начинайте со старших разрядов
- Проверяйте результат обратным вычитанием
- Для точных расчетов используйте дробную форму записи
- В программах учитывайте ограничения типов данных
Понимание и правильное применение правил суммирования позволяет избежать ошибок в математических расчетах и компьютерных программах. Эти фундаментальные принципы лежат в основе многих более сложных математических операций.